9044. Lonely island
There are many islands that
are connected by one-way bridges, that is, if a bridge connects islands a and b, then you can only use the bridge to go from a to b but you cannot
travel back by using the same. If you are on island a, then you select (uniformly and randomly) one of the islands that
are directly reachable from a through the one-way bridge and move to
that island. You are stuck on an island if you cannot move any further. It is
guaranteed that after leaving any island it is not possible to come back to
that island.
Find the island that you are
most likely to get stuck on. Two islands are considered equally likely if the
absolute difference of the probabilities of ending up on them is ≤ 10-9.
Input. The first line contains
three integers: the number of islands n (1 ≤ n ≤ 200000), the number of one-way bridges m (1 ≤ m ≤ 500000) and the index r (1 ≤ r ≤ n)
of the island you are initially on. Each of the next m lines contains
two integers ui and vi (1 ≤ ui, vi ≤ n) representing a one-way
bridge from island ui to vi.
Output. Print the index of the
island that you are most likely to get stuck on. If there are multiple
islands,then print them in the increasing order of indices (space separated
values in a single line).
|
Sample input |
Sample output |
|
5 7 1 1 2 1 3 1 4 1 5 2 4 2 5 3 4 |
4 |
SOLUTION
graphs - topological sort
Algorithm analysis
Let’s start the Kahn’s algorithm for topological sort. For each vertex v, compute the number of incoming
InDegree[v] and outgoing OutDegree[v] edges from it. Let us denote by prob[v] the probability to be at the vertex v. Initially, prob[r] = 1 for the starting vertex r,
for other vertices prob[v] = 0.
Next, for each vertex v, in the order of
topological sorting, iterate over the edges (v, to) and increase the value of prob[to] by prob[v] / OutDegree[v].
You can get stuck at the vertex v, for which OutDegree[v] = 0. Find the maximum value among
prob[v], for which OutDegree[v] = 0.
Example
Simulate Kahn’s algorithm for the graph
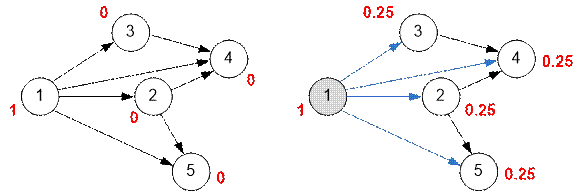
given in the problem. For each vertex of the graph we assign the probability to be there. Initially (figure on the left) the probability to be at all vertices is 0, except for the starting first,
for which probability is 1.
The first vertex in topological order will be 1. Four edges comes out of it, therefore the probability prob[1] = 1 will be
divided between 4 vertices: the value prob[1] / 4 =
0.25 should be added to prob[2], prob[3], prob[4] and prob[5].
Next,
vertex 2 will be added to the topological order. Two edges come out of it. prob[2] / 2 = 0.125 should be added to prob[4] and prob[5] (left figure
below). The next vertex will be 3. One edge comes out of it. Add prob[3]
/ 1 = 0.25 to prob[4] (figure on the right). Then vertices 4 and 5 will be
processed, but they do not contain outgoing edges and the probabilities will
not be recalculated.
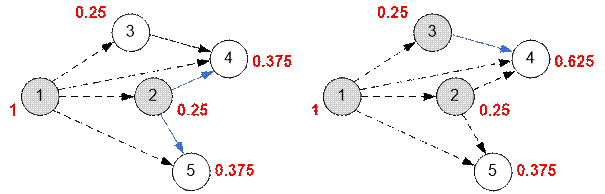
A dead-end vertex (that has no outgoing edges) with the maximum probability to
be there has
number 4. There is only one such vertex in the graph.
Algorithm realization
Declare a constant Epsilon.
#define EPS 1e-9
Store the graph in the adjacency
list graph. Declare the arrays.
vector<vector<int> > graph;
vector<int> InDegree, OutDegree;
deque<int> q;
vector<double> prob;
Read the input data. Initialize the arrays.
scanf("%d %d %d", &n, &m, &r);
graph.assign(n + 1, vector<int>());
InDegree.assign(n + 1, 0);
OutDegree.assign(n + 1, 0);
Read and construct a graph. For each vertex count the number of incoming and
outgoing edges.
for (i = 0; i < m; i++)
{
scanf("%d %d", &a,
&b);
graph[a].push_back(b);
OutDegree[a]++;
InDegree[b]++;
}
Push the vertices to the queue that have no incoming edges.
for (i = 1; i < InDegree.size(); i++)
if (InDegree[i] == 0) q.push_back(i);
The probability to be at vertex r is
1. For the remaining vertices the initial probability to be there is 0.
prob.resize(n + 1);
prob[r] = 1;
Run Kahn’s algorithm for finding a topological sort.
while (!q.empty())
{
Pop the vertex v from the queue. Iterate over the edges (v, to). There are OutDegree[v] edges come out from vertex v. The
probability to be at the vertex v equals to prob[v]. Therefore the probability of getting from v to to equals to prob[v] / OutDegree[v]. This probability should be added to prob[to].
v = q.front(); q.pop_front();
for (i = 0; i < graph[v].size(); i++)
{
to = graph[v][i];
prob[to] += prob[v] / OutDegree[v];
Decrease the number of
edges incoming the vertex v.
InDegree[to]--;
If no edge comes to the vertex to, push it to the queue.
if (InDegree[to] == 0) q.push_back(to);
}
}
Find the maximum value of
probability among prob[v] provided
that there is no exit from the island v.
mx = 0;
for (i = 1; i <= n; i++)
if (OutDegree[i] == 0 && prob[i] > mx) mx = max(mx, prob[i]);
Print the vertices
(there may be several of them) where the maximum
probability is achieved.
for (i = 1; i <= n; i++)
if (OutDegree[i] == 0 && fabs(prob[i] - mx) <= EPS)
printf("%d ", i);